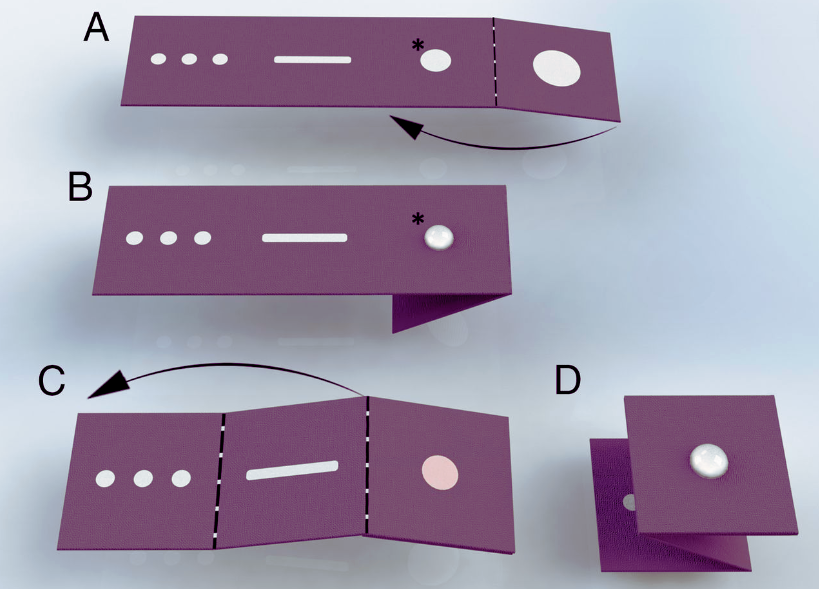
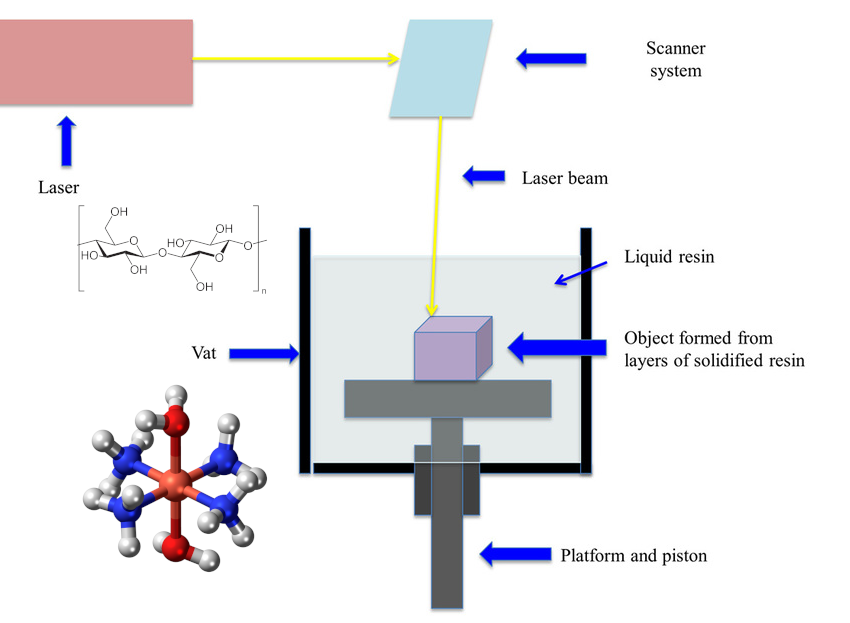
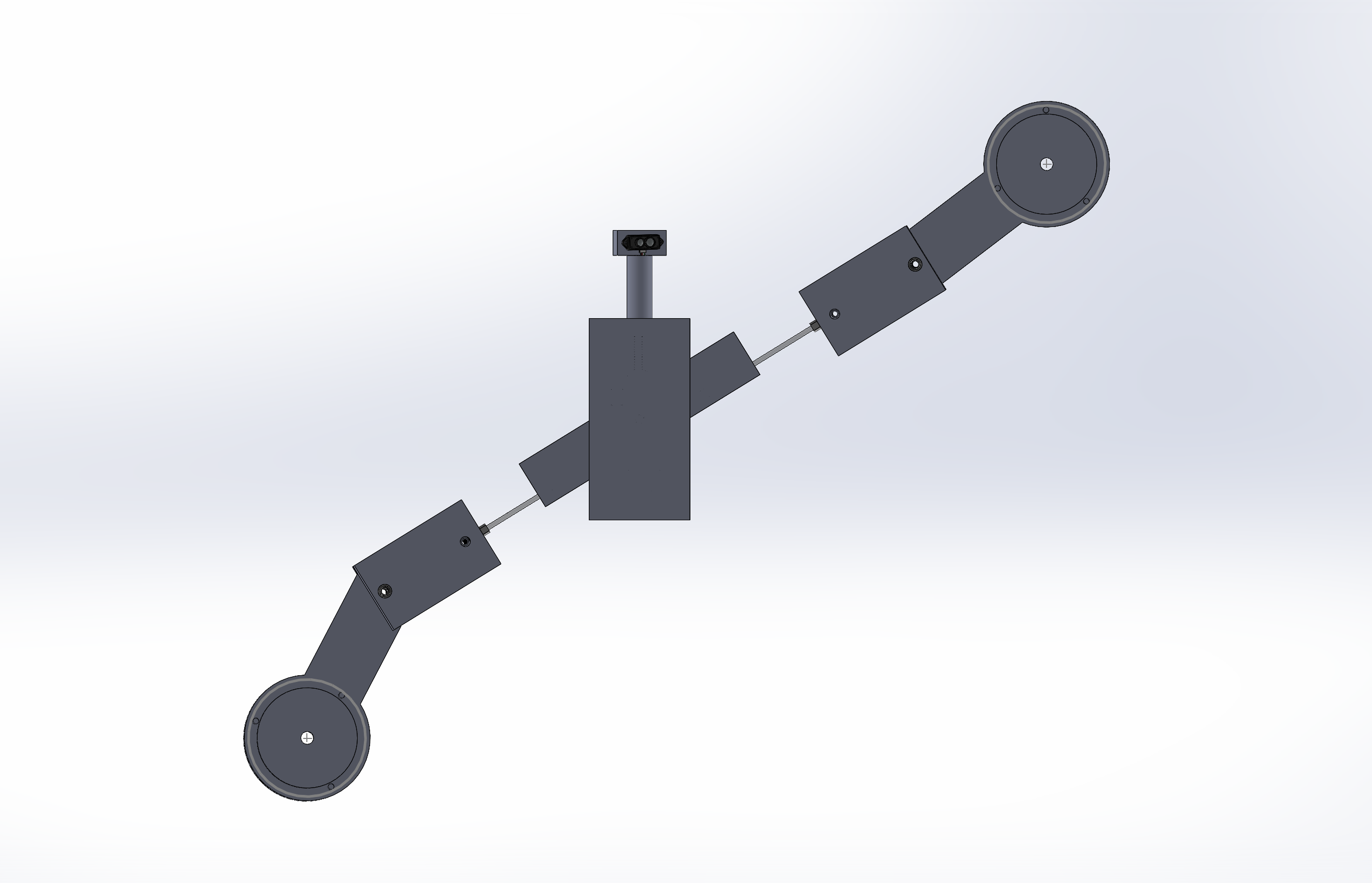
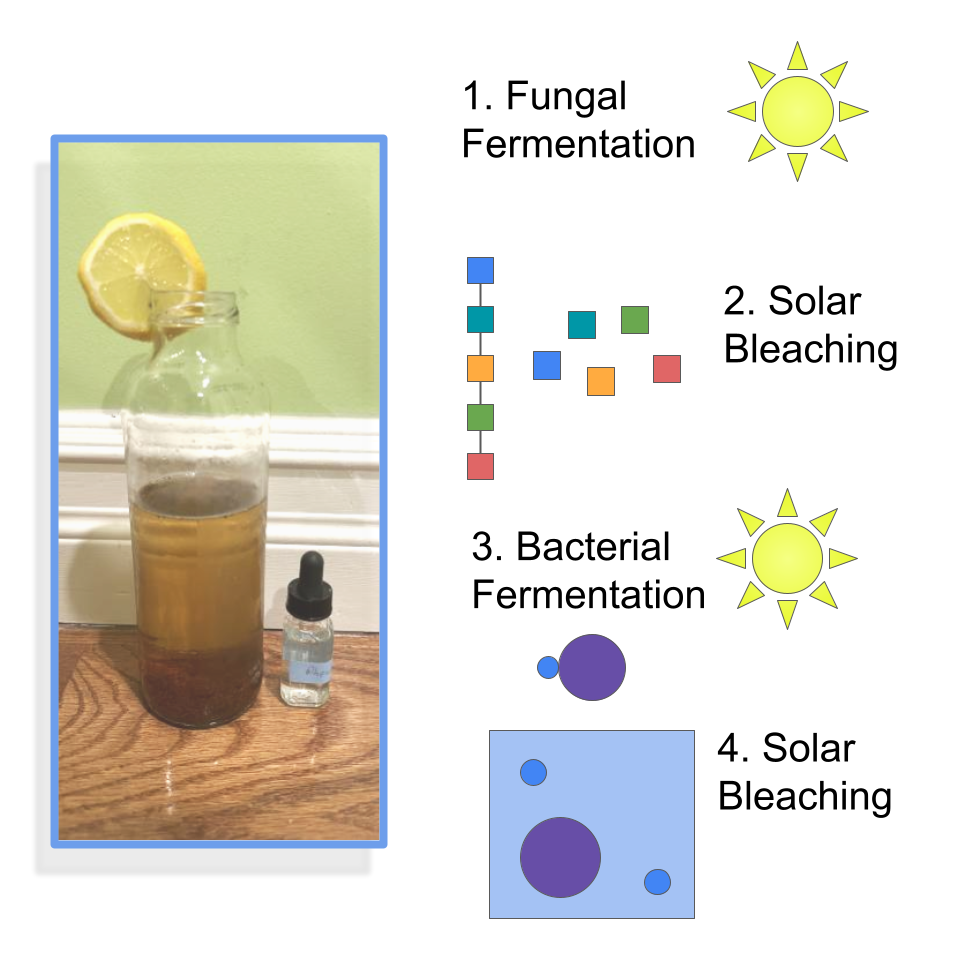
Rather than requiring students to have completed a research project before applying, THINK caters to students who have done extensive research on the background of a potential research project and are looking for additional guidance in the early stages of their project. The program is organized by a group of undergraduates at MIT.
the PREMISE
Selected finalists have weekly mentorship meetings with THINK team members for technical guidance, helpful resources, and updates on the projects progress and are given up to $1,000 in funding for their project. Additionally, if permitting, finalists are invited to a four-day all-expenses paid trip to MIT's campus, where they tour labs, present their research to MIT students and faculty, and hang out with members of the THINK team.
the PRIZE